Ein anderer Ansatz überträgt das Vorgehen bei der Entwicklung
des 1D-FFT Algorithmus.
Für
![]() ergibt sich
ergibt sich
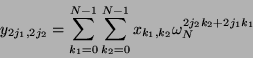 |
(17) |
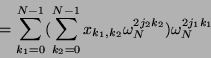
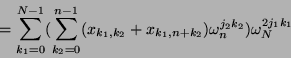
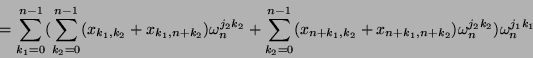
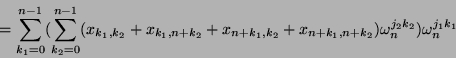
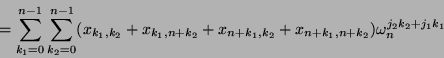
Die Berechnung der Matrix
![]() wird also auf die Berechnung der DFT der
wird also auf die Berechnung der DFT der ![]() -Matrix
-Matrix
![]() zurückgeführt.
Die Werte
zurückgeführt.
Die Werte
![]() ,
,
![]() und
und
![]() ergeben sich analog unter Berücksichtigung der auftretenden Gewichte.
ergeben sich analog unter Berücksichtigung der auftretenden Gewichte.
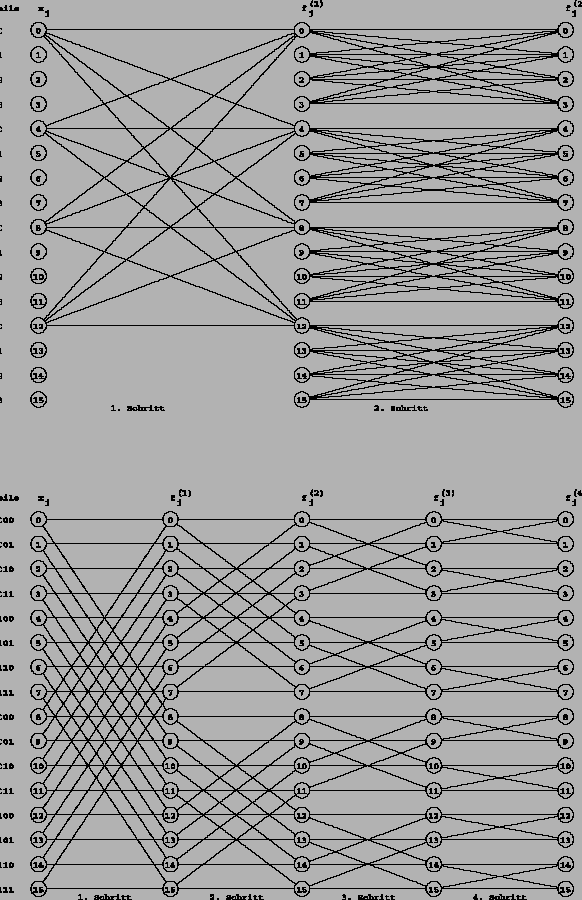
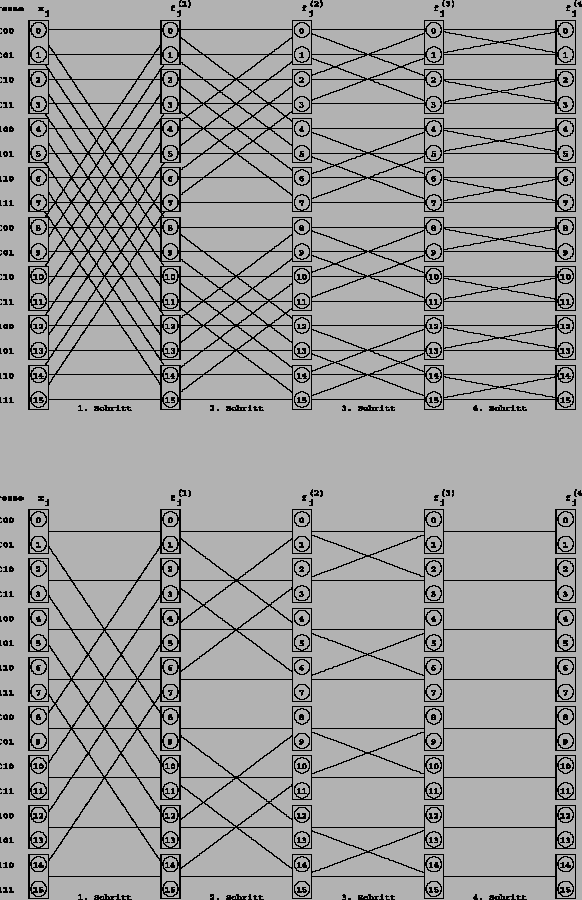
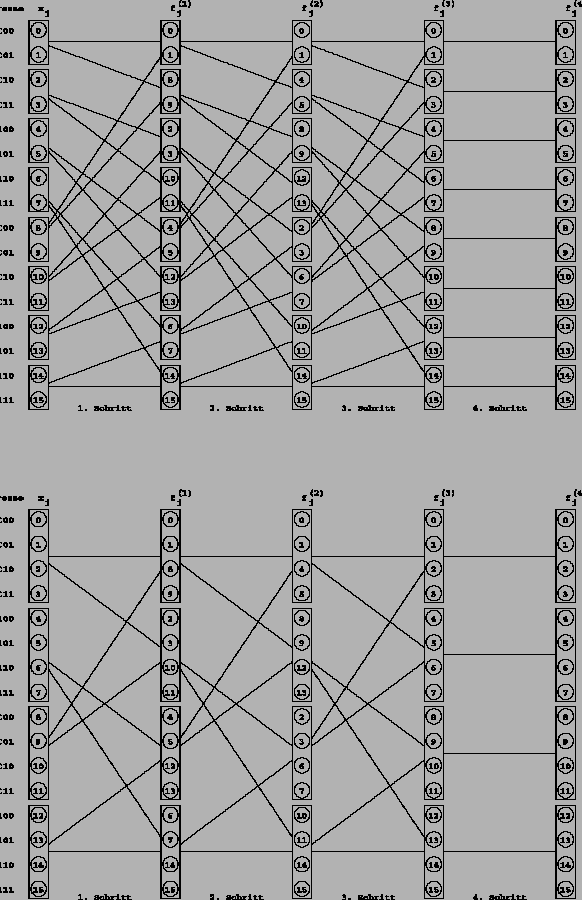
Die Datenflußstruktur dieses 2D-FFT Algorithmus läßt sich durch einen
![]() -dimensionalen Butterfly-Graph zur Basis 4
(Abbildung
-dimensionalen Butterfly-Graph zur Basis 4
(Abbildung ![]() ) beschreiben,
wenn die Eingangsmatrix wie folgt auf die Knoten verteilt wird
) beschreiben,
wenn die Eingangsmatrix wie folgt auf die Knoten verteilt wird
| 0 | 1 | 4 | 5 |
| 2 | 3 | 6 | 7 |
| 8 | 9 | 12 | 13 |
| 10 | 11 | 14 | 15 |
und in den Knoten folgende Funktionen
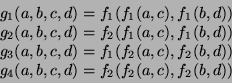 |
(18) |
für folgende Bereiche
verwendet werden, wobei ![]() und
und ![]() durch Gleichung
durch Gleichung ![]() gegeben sind.
gegeben sind.
 |
 |
 |
Die Entwicklung eines parallelen Algorithmus für ![]() Prozessoren, der
der Struktur dieses Butterfly-Graphen entspricht, verläuft wie folgt
Prozessoren, der
der Struktur dieses Butterfly-Graphen entspricht, verläuft wie folgt