Bei der schnellen Fourier-Transformation (FFT) handelt es sich
um einen Algorithmus zur Berechnung der DFT, der durch Anwendung des
Divide and Conquer-Paradigmas eine Zeitkomplexität
von ![]() erreicht.
Im folgenden soll der iterative FFT-Algorithmus und seine Datenflußstruktur
hergeleitet werden, da diese auch die Grundlage paralleler Implementierungen
bilden.
erreicht.
Im folgenden soll der iterative FFT-Algorithmus und seine Datenflußstruktur
hergeleitet werden, da diese auch die Grundlage paralleler Implementierungen
bilden.
Sei
![]() und
und ![]() .
.
Die Berechnung der Komponenten ![]() wird getrennt für gerade und ungerade
Indizes
wird getrennt für gerade und ungerade
Indizes ![]() betrachtet. Ziel ist jeweils, die Berechnung der Komponenten
betrachtet. Ziel ist jeweils, die Berechnung der Komponenten
![]() auf die Berechnung einer DFT der halben Länge
auf die Berechnung einer DFT der halben Länge ![]() zurückzuführen.
zurückzuführen.
Für
![]() gilt
gilt
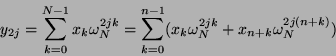 |
(7) |
Um die beiden Summanden zusammenzufassen betrachten wir
| (8) |
Analog erhalten wir für ungerade Indizes von y
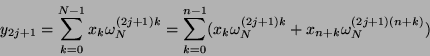 |
(10) |
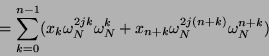 |
(11) |
Zum Zusammenfassen der Summanden benötigen wir noch, daß gilt
| (12) |
Damit ergibt sich für diesen Fall
Die Gleichungen ![]() und
und ![]() zeigen, daß wir
zeigen, daß wir
![]() durch die DFT der Länge n von
durch die DFT der Länge n von
![]() und
und
![]() durch die DFT von
durch die DFT von
![]() erhalten.
Für
erhalten.
Für ![]() läßt sich dieses Verfahren auf die beiden DFTs der Länge
läßt sich dieses Verfahren auf die beiden DFTs der Länge ![]() getrennt rekursiv anwenden.
getrennt rekursiv anwenden.
Dieses Vorgehen führt zu einem Butterfly-Graph
der Dimension
![]() zur Basis 2 als Datenflußgraph der FFT
(Abbildung
zur Basis 2 als Datenflußgraph der FFT
(Abbildung ![]() ).
).
Im ersten Schritt ergeben sich folgende Funktionen in den Knoten
| (14) |
Auf die Datenflußstruktur haben die Gewichte
![]() keine Auswirkung, so daß es im Folgenden ausreicht nur die beiden Typen
keine Auswirkung, so daß es im Folgenden ausreicht nur die beiden Typen
zu unterscheiden.
Durch das in jedem Schritt vorgenommene Anordnen der Ergebnisse zu
geraden Indizes in der oberen Hälfte des betrachteten Ausschnitts,
befindet sich das Ergebnis ![]() der DFT in der letzten Spalte
in der durch die gespiegelte
der DFT in der letzten Spalte
in der durch die gespiegelte
![]() -stellige Dualdarstellung von
-stellige Dualdarstellung von ![]() bestimmten Zeile (Bitreversal).
bestimmten Zeile (Bitreversal).